Intro to Algorithms

Welcome!
Girl Develop It is here to provide affordable and accessible programs to learn software through mentorship and hands-on instruction.
Some "rules"
- We are here for you!
- Every question is important
- Help each other
- Have fun
Welcome!
One extra-special rule for this class:
- Algorithms class gets confusing. Calling something challenging "obvious" can come out sounding a little bit condescending.
- If the point you're about to explain is TRULY obvious ("clear, self-evident, or apparent"), then by definition you shouldn't need to explain it.
GDI Philly is now on Slack!
Slack is a free, chat and messaging system available as either a web or native application for your desktop or mobile device. All our welcome to join our Slack team, but we need to add you! For an invitation, sign up here.
Introduce yourself
- Who are you?
- What do you hope to get out of this class?
- What's your favorite thing about the current season or time of year?
What we'll cover
- What is an algorithm?
- How to solve a problem with an algorithm, including:
- Stating a problem formally
- Solving the problem and expressing with psuedocode
- Proving correctness
- Analyzing runtime
- Introduction to Graph Theory
- Introduction to Sorting
- Introduction to Recursion
- Introduction to Greedy algorithms
What we won't cover
- A semester's worth of algorithms lectures
- Every algorithm ever
- ...or really, most algorithms (see Wikipedia)
- Rigorous proofs
- Advanced mathematical analysis
Warm-up exercise!
Your mission:
Find a way to shake the hand of every person in the room in the shortest time possible, but in a way that you can be confident you really did shake everyone's hand.
What are some approaches you came up with?
What is an algorithm?
An algorithm is an explicit, precise, unambiguous, mechanically-executable sequence of elementary instructions.
The word derives from the name of the 9th century Persian mathematician al-Khwarizmi.
What is an algorithm?
Is this sequence of instructions from the gnomes on South Park an algorithm?
Step 1: Collect underpants.
Step 2: ????
Step 3: Profit!
Verdict: No, this is not an algorithm. Step 2 is not specific, and a machine could not execute it.
What is an algorithm?
Is this sequence of instructions for taking out money from the ATM an algorithm?
Step 1: Insert card into ATM.
Step 2: Type your PIN on keypad.
Step 3: Enter an amount to withdraw less than your total balance.
Step 4: Receive money.
Verdict: Yes, this is an algorithm.
What is an algorithm?
Is this sequence of instructions from my shampoo bottle an algorithm?
Step 1: Lather.
Step 2: Rinse.
Step 3: Repeat.
Verdict: No, this is not an algorithm. Step 3 is ambiguous: what do we repeat, and until when?
Exercise!
Your mission: Think!
What are some algorithms from your everyday life?
What are some algorithms you've encountered while programming?
Why bother learning algorithms?
a.k.a. Why are you here?
- It's like weight lifting for your brain. Exercise the muscles now so that they're ready to use when you need them.
- It will help you think of techniques for solving problems.
- It will expose you to some classic problems in computer science, which are often referenced in articles, tech talks, and interview questions.
How to solve a problem with an algorithm
1. State the problem formally.
Be as clear as possible. Use generalized variables instead of specific examples or instances of the problem.
Bad: Sort some numbers like \((51, 62, 27, 3, 94)\).
Good: Sort an array of integers \(A_{1}, A_{2}, \ldots A_{n}\) in increasing order.
Exercise!
Can you transform this loosely-defined instance of a problem into a well-defined statement of a more generic problem?
Let's say I gave you five blocks with the weights of 1 pound, 2 pounds, 5 pounds, 8 pounds, and 10 pounds, respectively. Could you fill a sack with blocks so that its weight is exactly 21 pounds?
Interested in thinking more about this? It's called the "Knapsack Problem".
How to solve a problem with an algorithm
2. Find a solution to the problem*
* Note: this step in particular makes this list NOT an algorithm
You might solve the problem using known techniques, ingenuity, or a little bit of both.
Find a way to express your solution to others, perhaps through the use of pseudocode.
Pseudocode
- Uses the structure of formal programming languages and mathematics.
- Breaks algorithms down into primitive steps.
- The primitive steps may be written using mathematics, pure English, or an appropriate mixture of the two.
- Reveals the internal structure of the algorithm but hides irrelevant implementation details.
- Makes the algorithm much easier to understand, analyze, debug, and implement.
Pseudocode
Here is an algorithm for singing "99 Bottles of Beer on the Wall", for arbitrary values of 99:
BottlesOfBeer(\(n\)):
For i ← n down to 1
Sing "i bottles of beer on the wall, i bottles of beer,"
Sing "Take one down, pass it around,"
Sing "i − 1 bottles of beer on the wall."
Sing "No bottles of beer on the wall, no bottles of beer,"
Sing "Go to the store, buy some more, n bottles of beer on the wall."
Handshake problem
Find a way to shake the hand of every person in the room in the shortest time possible, but in a way that you can be confident you really did shake everyone's hand.
One possible solution:
Stand in two parallel lines facing each other. Shake hands with the person in front of you. Take a step to the left, where the last person at the end of the line moves to the beginning of the other line. Continue this process until you have shaken everyone's hand.
Handshake problem
Let's express it with pseudocode!
HandshakeWithEveryone(\(P[1 .. n]\)):
⟨⟨i represents the number of people you still need to shake hands with⟩⟩
for i ← n down to 2
⟨⟨shake hands⟩⟩
line1 ← P[1 .. n/2]
line2 ← P[n/2 + 1 .. n]
ShakeHands(line1, line2);
⟨⟨shift over one, and wrap the last person⟩⟩
P’[n] ← P[1]
for j ← n down to 2
P’[j-1] = P[j]
P ← P’
Exercise!
Write pseudocode that prints the lyrics of the song "BINGO" for arbitrary long names of dogs.
There was a farmer who had a dog
And BINGO was his name-o
B-I-N-G-O, B-I-N-G-O, B-I-N-G-O
And BINGO was his name-o
There was a farmer who had a dog
And BINGO was his name-o
(clap)-I-N-G-O, (clap)-I-N-G-O, (clap)-I-N-G-O
...
How to solve a problem with an algorithm
3. Prove your algorithm is correct.
- We must convince our audience (and ourselves!) that the algorithm actually does what it's supposed to do.
- The algorithm must be correct for all possible inputs. It's not enough to show that the algorithm does the right thing on some example input.
- Usually requires a formal, mathematical proof of correctness.
Mathematical proofs
Just kidding. We're totally not going to cover this today; it would need a class of its own.
In lieu of knowing how to construct formal proofs, you can do a few other things in practice:
- Try to reason, even informally, about why your algorithm is correct.
- Explain your algorithm to a peer. You'll have to be very clear to convince your peer, and your peer's feedback can be valuable.
- If you're coding, write unit tests that cover all possible inputs.
How to solve a problem with an algorithm
4. Analyze the runtime of your algorithm.
(and/or storage space needed to execute the algorithm)
We want to communicate how long our algorithm will take to execute, and we want to be able to compare it against other algorithms claiming to do the same task.
It's impossible to predict what size input your algorithm is going to have to operate on, so we express runtime in terms of the size of the input.
Analyzing runtime
Let's consider the expression \(2x + 7\) for different inputs of size \(x\):
| If \(x=0\): | \(2*0 + 7 = 7\) |
| If \(x=1\): | \(2*1 + 7 = 9\) |
| If \(x=10\): | \(2*10 + 7 = 27\) |
| If \(x=100\): | \(2*100 + 7 = 207\) |
| If \(x=10000\): | \(2*10000 + 7 = 20007\) |
The constant \(7\) becomes less and less a part of the answer as the size of \(x\) gets bigger and bigger.
Analyzing runtime
Asymptotic analysis is the method of characterizing a mathematical function by how it trends as the input size approaches infinity.
In computer science, we use big O notation to talk about asymptotic growth. We use it to capture the worst case run time of your algorithm.
You say: "two ex plus seven is big oh of ex"
Analyzing runtime
To find the big O function, you can often "drop" terms from your expression that grow significantly slower than the leading term.
In practice, you shouldn't have to think too much about complicated equations, but it's important to understand where the idea of "big O" comes from.
Analyzing runtime
For your purposes, it's probably best to think about big O conceptually.
Example 1: What is the first element of the array \(A[1 .. n]\)?
Algorithm: Simply return \(A[1]\), regardless of the size of the number of elements, \(n\).
This took us a constant amount of time, a.k.a. \(O(1)\).
Analyzing runtime
Example 2: What is the largest number in the array \(A[1 .. n]\)?
b ← -infinity
for i ← 1 to n
if A[i] > b
b ← A[i]
return b
We had to loop over every element of the array, so we had to look at all \(n\) inputs.
This took us a linear amount of time, a.k.a. \(O(n)\).
Analyzing runtime
Example 3: Does the array \(A[1 .. n]\) contain any duplicates?
for i ← 1 to n
for j ← 1 to n
if i = j
continue
else if A[i] = A[j]
return true
return false
We have two nested loops over the array.
This took us a quadratic amount of time, a.k.a. \(O(n^{2})\).
Comparing runtimes
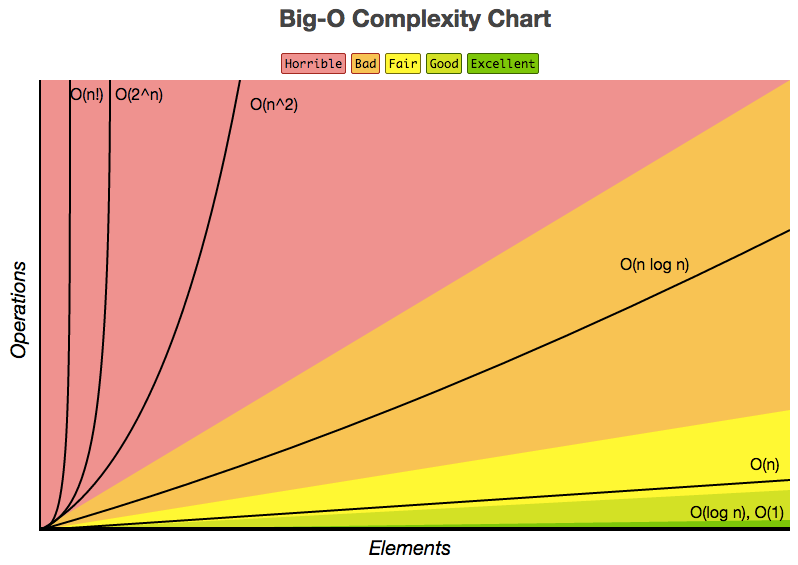 Source: http://bigocheatsheet.com
Source: http://bigocheatsheet.com
How to solve a problem with an algorithm
Let's review what we've learned!
- State the problem formally.
- Find a solution to the problem.
- Prove your algorithm is correct.
- Analyze the runtime of your algorithm.
Got it? Good. Now let's have some fun!
Graph Theory
A graph is defined as \(G = (V, E)\), where \(V\) is a set of objects called vertices (singular: vertex), and \(E\) is a set of edges joining pairs of vertices.
Graphs represent a set of concepts and how they are related to each other, and they can be used to model many concepts.
Graph Theory in Real Life
Transit maps, like PATCO:
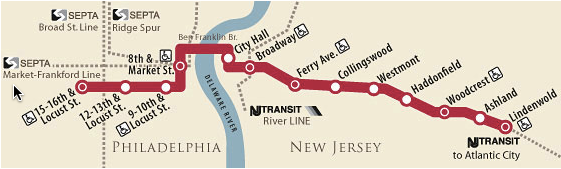
Graph Theory in Real Life
Flight maps, like for Spirit Airlines:
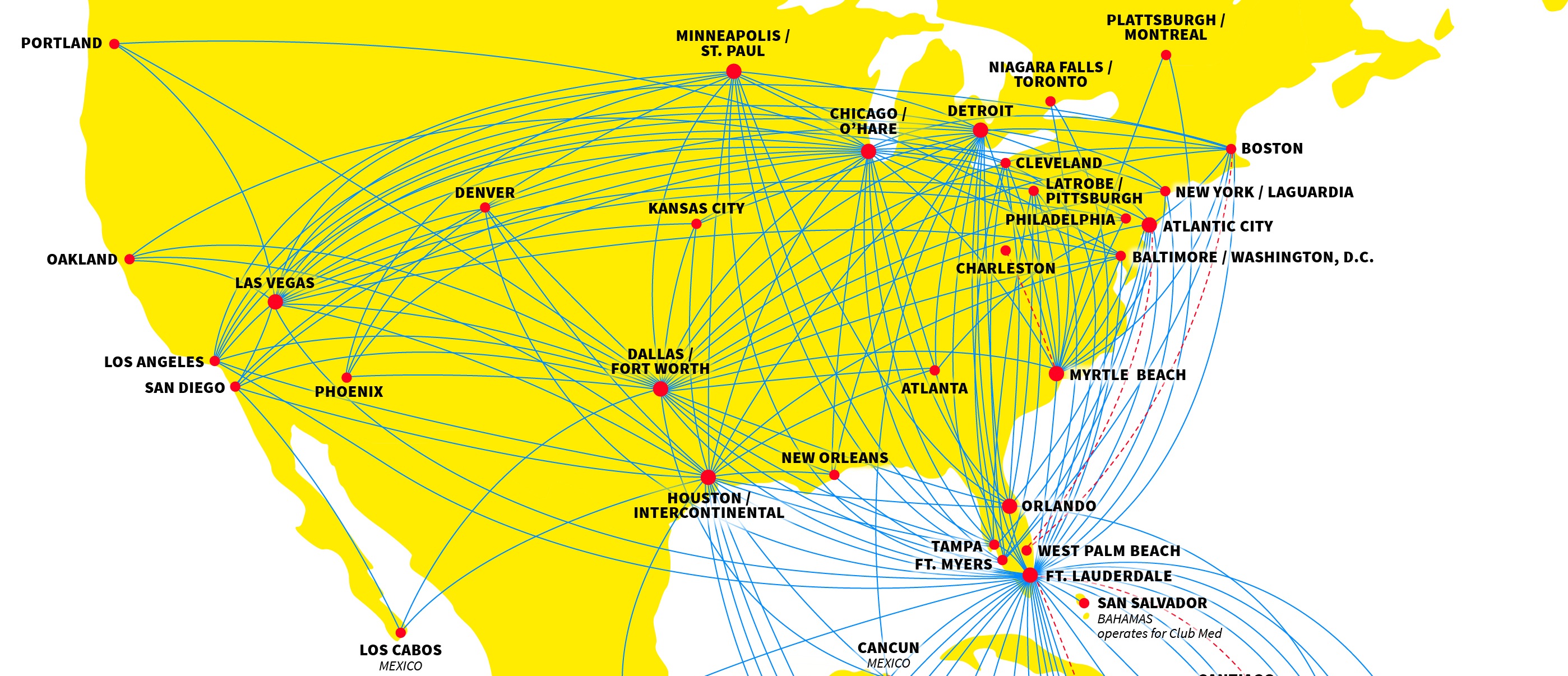
Graph Theory in Real Life
The possibilities are endless. Here's a few more:
- Wikipedia articles and the hyperlinks between them
- Users or objects on a social media site and the "friendships" or "likes" between them
- Relationships of movie actors, so as to play Six Degrees of Kevin Bacon
Once you have modeled your problem as a graph, then you can use Graph Theory to solve your problem.
Bridges of Königsberg
The city of Königsberg in Prussia was set on both sides of the Pregel River, and included two large islands which were connected to each other and the mainland by seven bridges.
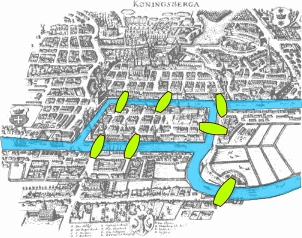
Bridges of Königsberg
The big question:
Is it possible to find a walk through the city that would cross each bridge once and only once?

Exercise: Try it!
Bridges of Königsberg
The key piece of intuition:
It follows that every vertex (except for the start and the finish) must have an EVEN number of edges touching it.
Bridges of Königsberg
Definition: We call the number of edges coming out of a vertex the degree of the vertex.
Definition: A walk or a path is a sequence of vertices and edges, where each edge's endpoints are the preceding and following vertices in the sequence.
Definition: A tour or a circuit is a walk where the vertices at the beginning and end of the walk are the same.
Bridges of Königsberg
This problem was studied by Leonard Euler (pronounced "oil-er") in 1735 and laid the foundations for graph theory and topology.
In Euler's honor, we say that a graph that contains exactly zero or two vertices of odd degree has an Eulerian path (or walk).
If the start and endpoints are the same vertex, then it is called an Eulerian tour (or circuit).
Bridges of Königsberg

Conclusion: Since the graph corresponding to the Königsberg bridges has four vertices of odd degree, it cannot have an Eulerian path.
Graph Exercise 1
Find an Eulerian walk for the graph below:
Is it possible to find an Eulerian circuit?
Graph Exercise 2
Definition: A graph is called complete if every pair of distinct vertices has an edge between them. (No loops from a vertex back to itself.)
Draw the complete graph on 0 vertices, 1 vertex, 2 vertices, 3 vertices, 4 vertices, and 5 vertices. (Hint: if 0 and 1 are stumping you, skip over them and start from 2)
Tree traversal
Definition: A graph is connected if it is in one piece; that is, if a path exists between any pair of vertices.
Definition: A graph is a tree if every two vertices are connected by exactly one path. Another way to define a tree is to say that there are no circuits or cycles from one vertex back to itself.
Tree traversal
Most people in the room are already VERY familiar with one tree we talk about a lot in GDI classes:
Tree Traversal
Suppose we have a connected tree where each vertex has a label, and we're looking for a vertex with a particular label.
There are two well-known algorithms that we can use:
- Depth-first search
- Breadth-first search
Tree traversal
Depth-first search (DFS): Starting from some vertex, explore as far as possible down each branch before backtracking.
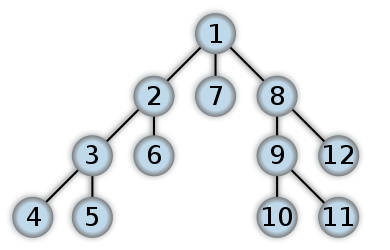
Tree Traversal
Breadth-first search (BFS): Starting from some vertex, fan out to as many vertices as possible before exploring deeper into the tree.
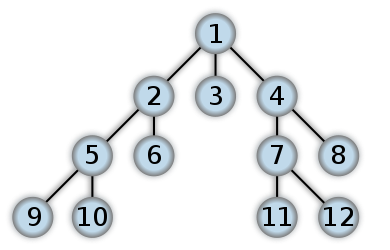
Tree Traversal
When you should use DFS versus BFS is something that varies on the nature of the graph you're searching.
If the graph expands rapidly, then it may take too much memory to remember all the nodes you're fanning through for BFS.
If the graph is very deep, then it might take too much time getting lost down individual paths for DFS.
Exercise
Let's say you were looking for the vertex "f". How many vertices do you have to check against when searching by DFS? by BFS?
Traveling Salesman Problem
The famous traveling salesman problem asks the following question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?
This can be modeled as a graph where the cities are the vertices, the connections are the edges, and the distances are weights or labels on the edges.
Traveling Salesman Problem
Traveling Salesman Problem

Traveling Salesman Problem
Although we don't nearly have enough time to fully go into WHY, it's worth pointing out why this problem is famous: it's one of a set of problems that are called NP-hard.
Only very long-running (think: exponential!) solutions have been found. If you find an algorithm that takes only a polynomial amount of time, you will be a very rich and famous celebrity of computer science.
Graph Theory: Wrap up
You can use graphs to model lots of real-world problems, and then apply algorithms to the resulting graph to solve those problems.
If you like this stuff, then you might want to look into more Graph Theory problems, such as:
- Four Color Theorem
- Hamiltonian paths
- Minimum spanning tree
- Max Flow / Min Cut
Sorting Algorithms
There are lots of ways to sort things! Here's some:
- Selection sort - repeatedly find the smallest element and append to the sorted list
- Insertion sort - repeatedly take the first element and find it's place in the sorted list
- Quick sort - repeatedly picks a pivot point and finds elements smaller and larger than the pivot
- Merge sort - divide into small groups and repeatedly merge the sorted sub-lists
- Bubble sort - repeatedly compare pairs and swap if necessary until the list is sorted
Sorting Algorithms: Visualization!
Stand-up exercise!
Your mission:
Take a card with a number. Sort yourselves in numeric order following the Merge Sort algorithm.
We'll walk through it together!
Merge Sort Part 1: Divide
- Start as one unorganized clump of \(n\) humans.
- Split into two even groups.
- Each of the two groups splits into two groups (total: four groups of \(n/4\) humans).
- Continue splitting up (and keep track of the splits!) until there are \(n\) groups, each with \(1\) human.
Merge Sort Part 2: Merge
- Each pair of humans that was the last to break apart should get back together into a group of 2.
- Compare your two numbers. The person with the smaller number should move to the left side, and the person with the larger number should move to the right side.
- Now you have a group of 2 that is sorted. All around the room, we should have sorted groups of 2.
- Next, two groups of size 2, which originally split apart from each other, need to merge...
Merge Sort Part 2: Merge
- Two sorted groups approach each other.
- From EACH sorted group, the person with the SMALLEST number should step forward. These two people should compare their numbers.
- Whoever has the smaller number (Person A) should move to the side to start a new sorted line; whoever has the larger number (Person B) should stay put and wait for another comparison.
- The next smallest number holder from Person A's group should step forward and compare numbers with Person B.
- Continue comparing until your two groups have merged into one sorted group.
Merge Sort Part 2: Merge
We'll continue this process until everyone has merged into a SINGLE line!
Let's go try it!
Reduction
Reducing one problem X to another problem Y means to write an algorithm for X that uses an algorithm for Y as a black box or subroutine.
The correctness of the resulting algorithm cannot depend in any way on how the algorithm for Y works. The only thing we can assume is that the black box solves Y correctly.
Think of the black box Y as MAGICAL.
Reduction
We use reductions every day in real life, and they're very common in programming. For example, consider my husband's commute:
Problem: Get from our house to work.
- Walk from our house to the PATCO station.
- Ride PATCO. (black box!)
- Walk from 12-13/Locust to work
Exercise
Can you think of something you do in real life or something you had to program where you used a subroutine or black box?
Recursion
Recursion is a particularly powerful kind of reduction, which can be described loosely as follows:
- If the given instance of the problem is small or simple enough, just solve it.
- Otherwise, reduce the problem to one or more simpler instances of the same problem.
Recursion
When we reduce problem X to smaller versions of problem X, we rely on those smaller versions of problem X magically solving themselves.
My teacher used to call this the magic of the "Recursion Fairy".
Recursion
To solve a problem with recursion:
- You need to solve some sort of base case. This often means solving the problem for an input of size 0 or 1.
- You need to divide up the problem into smaller parts and pass them to the recursion fairy.
- You need to be able to use the results that the recursion fairy gives you.
- Don't try to recurse over an infinite list of items.
Merge Sort, revisited
Recall our human merge sort? We split into smaller and smaller groups, and then merged back together in a sorted order.
What you were actually doing is solving the sorting problem using recursion!
Merge Sort, revisited
When we had individual groups of size 1, that was our base case.
When we looked at two already-sorted smaller lines, we were trusting that they were sorted because the recursion fairy knew how to properly sort them.
We had a procedure to take the result from the recursion fairy and combine into a larger sorted list.
Merge Sort, revisited
MergeSort(Number_1, Number_2, ... Number_n):
if n = 1
return (Number_1); ⟨⟨Your list is already sorted⟩⟩
else
⟨⟨Recursively sort two smaller lists⟩⟩
sorted_left_list = MergeSort(Number_1, Number_2, ... Number_n/2)
sorted_right_list = MergeSort(Number_(n/2 + 1), ... Number_n)
⟨⟨Merge the sorted sublists⟩⟩
final_list = new Array
while sorted_left_list and sorted_right_list are not empty
if first(sorted_left_list) <= first(sorted_right_list)
remove first(sorted_left_list) from sorted_left_list
append first(sorted_left_list) to final_list
else
remove first(sorted_right_list) from sorted_right_list
append first(sorted_right_list) to final_list
return final_list
Merge Sort, Revisited
This tree represents how we tackled sorting with merge sort. We started at the top, divided into two until we reached our base case, and then traveled back up the tree merging lists back together.
Fun fact: the height of this tree of n vertices is log n. This is part of why the run time of Merge Sort is O(n log n).
Recursion vs. Iteration
Many problems with recursive solutions can also be solved without recursion, usually by looping or iterating.
People often debate which is better for problem solving: recursion or iteration. The short answer is...
Recursion vs. Iteration
It depends on the programming language.
Some languages like C have a lot of overhead when they call functions. If you have to call the same function over and over and over, you can quickly run out of stack space (the way that the computer remembers the order of function calls).
Recursion vs. Iteration
It depends on the problem.
Sometimes a recursive algorithm is more succinct and better captures the algorithm's intent.
Some classes of problems feel like they're just MADE for a recursive solution, like problems about trees in graph theory.
Recursion: DFS
Remember Depth-First Search that we talked about before? We can express that as a recursive algorithm.
DFS(graph \(G\), vertex \(v\), searchterm \(i\)):
if v does not exist
return false
else if the label of v matches i
return true
else
for every edge from v to other vertex u
return DFS(G, u, i)
Recursion: DFS
We've reduced the problem of finding label \(i\) in a huge graph \(G\) to finding label \(i\) in a slightly smaller graph, \(G\) less the vertex \(v\).
Once we have the answer from the subgraph, we can simply return it.
And it just works.
Thanks, Recursion Fairy.
Exercise
Consider the following problem regarding the population of rabbits:
- Each pair of rabbits produces a new pair of offspring each month
- Rabbits become fertile in their second month of life
- Old rabbits never die
If a pair of newborn rabbits are introduced in January, how many pairs of rabbits will there be at the end of the year?
Recursion: Fibonacci
Perhaps it's useful to know that that problem was posed in 1202 by Leonardo Fibonacci...
We can express how to calculate a term in the Fibonacci series recursively!
Fibonacci(\(n\)):
if (n < 2)
return n
else
return Fibonacci(n-1) + Fibonacci(n-2)
Recursion: Fibonacci
Something to keep in mind: often with recursion, you repeat the same calculations over and over again as you recurse.
If you have enough storage space, you can save some time by saving values as you calculate them. This is called memoization.
Recursion: Wrap up
You can often solve problems by reducing a problem to another problem.
If you reduce a problem to one or more smaller instances of itself then you are performing recursion.
Solve for a small base case and be able to combine and return the results of the smaller, magical pieces.
Recursion: Wrap up
Interested in solving problems with recursion? Look into some other problems that have elegant recursive solutions, such as:
- Towers of Hanoi
(did you get to play with it before class?) - Binary search
- Filesystem traversal
- Lots of other algorithms that can be expressed recursively!
Special topics
If there's one thing I learned in computer science classes, it's that the speaker always talks about their own research last if they have extra time.
Today I'm going to teach you about coin sets and greedy algorithms.
Quick exercise
Let's say you are a cashier and you owe somebody 43 cents.
1. What is the maximum number of coins you could give to the person?
2. What is the minimum number of coins you could give to the person?
Coin sets
We can characterize the denominations of the coins of the US with an array of values called a coin set:
You'll use the minimum number of coins by always choosing the largest denomination coin that is not larger than the amount you have left to make.
Greedy algorithms
A greedy algorithm is an algorithm that always makes the locally-optimal choice with the hopes of finding a global optimum.
Sometimes, a greedy algorithm finds an optimal solution.
For many problems, a greedy algorithm will NOT produce a correct solution. But sometimes it produces a close-enough approximation to the optimal result.
Non-Greedy coin sets
Instead of the standard US coin set, what if you had the following coin set:
Spoiler alert: this is a coin set where the greedy algorithm WON'T always work. There is at least one counterexample to greediness.
Exercise: Find an amount of change that you CAN make greedily. Find an amount of change that you CANNOT make greedily.
Non-Greedy coin sets
Antarctica Dream-Dollars, the official currency of Nadiria, the lost colony of Antactica, is a fun example of a non-greedy coin set:
Were the coin set creators to have left off the 365 or were they to include rather the denomination 364, they would have a greedy coin set!
Non-Greedy coin sets
A real-life example of a non-greedy coin set is the English system of currency from pre-1971:
Final Wrap Up!
- What is an algorithm?
- How to solve a problem with an algorithm, including:
- Stating a problem formally
- Solving the problem and expressing with psuedocode
- Proving correctness
- Analyzing runtime
- Introduction to Graph Theory
- Introduction to Sorting
- Introduction to Recursion
- Introduction to Greedy algorithms
Recommended Textbooks
Introduction to Algorithms - Cormen, Leiserson, Rivest, Stein (available on Amazon)
About this book: a.k.a. "CLRS", a well-known advanced undergraduate textbook for a course in algorithms
Discrete Mathematics and its Applications - Rosen (available on Amazon)
About this book: a well-known junior undergraduate textbook for a course in discrete mathematics, which is generally an expected prerequisite for algorithms
Recommended Textbooks
Introduction to Graph Theory - Robin J. Wilson
(available on Amazon)
About this book: An advanced undergraduate textbook for a course dedicated to the study of graph theory.
Wikipedia
Jeff Erickson's Algorithms notes
These notes provided some of the backbone of this class. Some definitions and examples in these slides were taken directly from these notes. Many thanks to Jeff for making his not-a-textbook an available resource.
http://www.cs.illinois.edu/~jeffe/teaching/algorithms
Take another GDI Class!
With Algorithms in your brain, the world is your oyster! Check out the Suggested class sequences on our Meetup.
Get Involved
- Join Slack community
- Teaching assist
- Teach something
- Mentor or be mentored
All forms here (on Meetup)
Thank you for attending!
We value your feedback and are always trying to improve.